Solve the following :

Question:
An aero plane has to go from point $A$ to another point $B, 500 \mathrm{~km}$ away due to $30^{\circ}$ east of north. A wind is blowing due north at a seed of $20 \mathrm{~m} / \mathrm{s}$. The air speed of the plane is $150 \mathrm{~m} / \mathrm{s}$.

(a) Find the direction in which the pilot should head the plane to reach the point $B$.

(b) Find the time taken by the plane to gr from $A$ to $B$.

Solution:

(a)

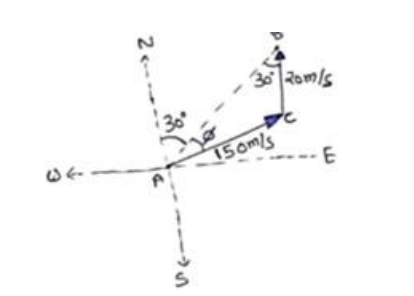
In $\triangle \mathrm{ACB}$

Using sin formula

$\frac{20}{\sin \phi}=\frac{150}{\sin 30^{\circ}}$

$\sin \emptyset=\frac{1}{15}$

$\emptyset=\sin ^{-1}\left(\frac{1}{15}\right)$ east of the line $A B$

(b)

$\emptyset=3^{\circ} 48^{\prime}$. Angle between two vector $=30+3^{\circ} 48^{\prime}$

$R=\sqrt{A^{2}+B^{2}+2 A B \cos \theta}$

$\mathrm{R}=167 \mathrm{~m} / \mathrm{s}$

Time $=\frac{\text { distance }}{\text { speed }}=\frac{500 \times 10^{3}}{167}$

$=2994 \mathrm{sec}$

$\mathrm{T}=60 \approx 50 \mathrm{~min}$

Solve the following :

Leave a comment

All Study Material