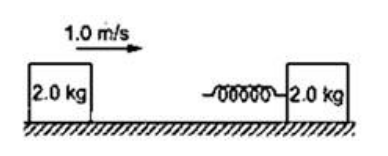
Question:
A block of mass $2.0 \mathrm{~kg}$ is moving on a frictionless horizontal surface with a velocity of $1.0 \mathrm{~m} / \mathrm{s}$ towards another block of mass kept at rest. The spring constant of the spring fixed at one end is $100 \mathrm{~N} / \mathrm{m}$. Find the maximum compression of the spring.
Solution:
We know that for the spring,
$a=-\omega^{2} x$
$a=\frac{-k}{m} \times x$
$a=\frac{-100}{2} \times x=-50 x$
Use law of kinematics,
$v^{2}=u^{2}+2 a x \quad\{u=1 m / s\}$
$0=1-2.50 . x^{2}$
$x=\sqrt{\frac{1}{2 \times 50}}=\sqrt{\frac{1}{100}}=\frac{1}{10}=0.1 \mathrm{~m}$
$x=10 \mathrm{~cm}$
