Question:
Light in certain cases may be considered as a stream of particles called photons. Each photon has a linear momentum $\mathrm{h} /{ }^{\lambda}$ where $\mathrm{h}$ is the Planck's constant and $\lambda$ is the wavelength of the light. A beam of light of wavelength $\lambda$ is incident on a plane mirror at an angle of incidence ${ }^{\theta}$. Calculate the change in the linear momentum of a photon as the beam is reflected by the mirror.
Solution:
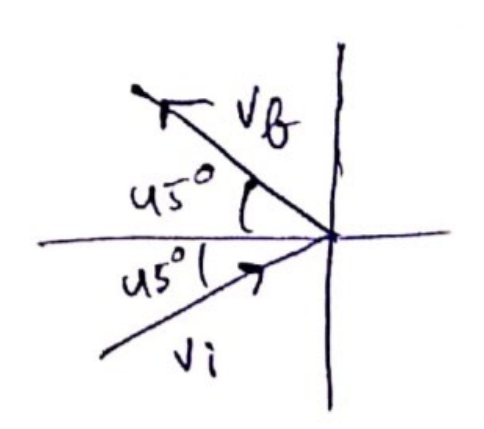
$p_{i}=\frac{h}{\lambda}(\cos \theta \hat{\imath}+\sin \theta \hat{\jmath})$
$p_{f}=\frac{h}{\lambda}(-\cos \theta \hat{\imath}+\sin \theta \hat{\jmath})$
$\Delta \vec{p}=\vec{p}_{i}-\vec{p}_{f}=\frac{2 h}{\lambda} \cos \theta \hat{i}$
$|\Delta \vec{p}|=\frac{2 h}{\lambda} \cos \theta$
