A man of mass $M$ having a bag of mass $m$ slips from a roof of a tall building of height $\mathrm{H}$ and starts falling vertically. When at a height $h$ from the ground, he notices that the ground below him is pretty hard, but there is a pond horizontal from the distance $x$ from the line of fall. In order to save himself he throws the bag horizontally in the direction opposite to the pond. Calculate the minimum horizontal velocity imparted to the bag so that the man lands in water. If the man just succeeds to avoid hard ground, where will the bag land?
When he throws a bag to left, momentum is conserved. $m v_{b}=M V_{M}$
$V_{b}=$ velocity of bag
$V_{M}=$ speed of man
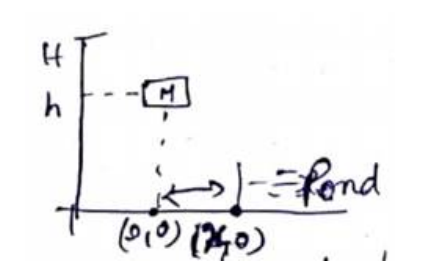
Let pond start from $\left({ }^{x_{i}}\right)$
Time to reach height $\mathrm{h}=\sqrt{2(H-h) / g}=t_{h}$
Time to reach ground, $t_{g}=\sqrt{2 H / g}=t_{g}$
Time taken by man $=t_{g}-t_{h}=t_{M}$
$=\sqrt{\frac{2}{g}}(\sqrt{H}-\sqrt{H-h})$
COM of the system will be at $(0,0)$ after he reaches ground (let bag reach ${ }^{x_{1}}$ from origin) $\left({ }^{x_{1}}, 0\right.$ )
$\therefore 0=\frac{M \times x+m \times x_{1}}{M+m}$
$x_{1}=\frac{-M}{m} x$
From law of kinematics
$x_{M}-0=V_{M} t \quad\left\{x_{M}=x\right\}$
$x=V_{M} t_{M}=v\left(t_{g}-t_{h}\right)$
$V_{M}=\frac{x}{t_{g}-t_{h}}=x \sqrt{\frac{g}{2}}(\sqrt{H}-\sqrt{H-h})^{-1}$
$v_{b}=\frac{M}{m} V_{M}=\frac{M x}{m} \sqrt{\frac{g}{2}} \frac{1}{\sqrt{H}-\sqrt{H-h}}$
