A small block of mass $100 \mathrm{~g}$ is pressed against a horizontal spring fixed at one end to compress the spring through $5.0 \mathrm{~cm}$ (figure 8-E11). The spring constant is $100 \mathrm{~N} / \mathrm{m}$. When released, the block moves horizontally till it leaves the spring. Where will it hit the ground $2 \mathrm{~m}$ below the spring?
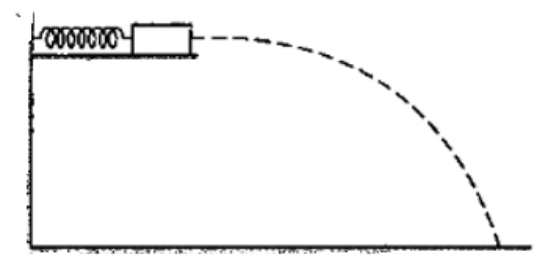
By law of conservation of energy:
$\frac{1}{2} m v^{2}=\frac{1}{2} k x^{2}$
$v=1.58 \mathrm{~m} / \mathrm{s}^{2}$
Now, projectile motion
$y=(u \sin \theta) t-\frac{1}{2} g t^{2}$
$\theta=0^{0}, y=-2$
$t=0.63 \mathrm{sec}$
and
$x=(u \cos \theta) t=1.58 \times 0.63$
$x=1 \mathrm{~m}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
