Question:
Two blocks of masses $m_{1}$ and $m_{2}$ are connected by a spring of spring constant $k$. The block of mass $m_{2}$ is given a sharp impulse so that it acquires a velocity $v_{0}$ towards right. Find (a) the velocity of the center of mass, (b) the maximum elongation that the spring will suffer.
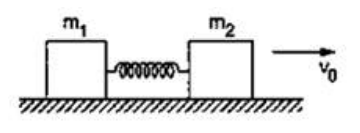
Solution:
(a) $V_{C O M}=\frac{m_{2} \times V_{0}+m_{1}(0)}{m_{1}+m_{2}}=\frac{m_{2} V_{0}}{m_{1}+m_{2}}$
(b) Use C.O.E.L
$\frac{1}{2} m_{2} V_{0}^{2}-\frac{1}{2}\left(m_{1}+m_{2}\right) V_{C O M}^{2}=\frac{1}{2} u x^{2}$
$x=\sqrt{\frac{m_{2} V_{0}^{2}-\left(m_{1}+m_{2}\right) \frac{m_{2}^{2} V_{0}^{n}}{\left(m_{1}+m_{2}\right)^{2}}}{k}}$
$x=\sqrt{\frac{m_{1} m_{2}}{\left(m_{1}+m_{2}\right) k}} V_{0}$
