Figure shows a rough track, a portion of which is in the form of a cylinder of radius $\mathrm{R}$. With what minimum linear speed should a sphere of radius $r$ be set rolling on the horizontal part so that it completely goes round the circle on the cylindrical part.
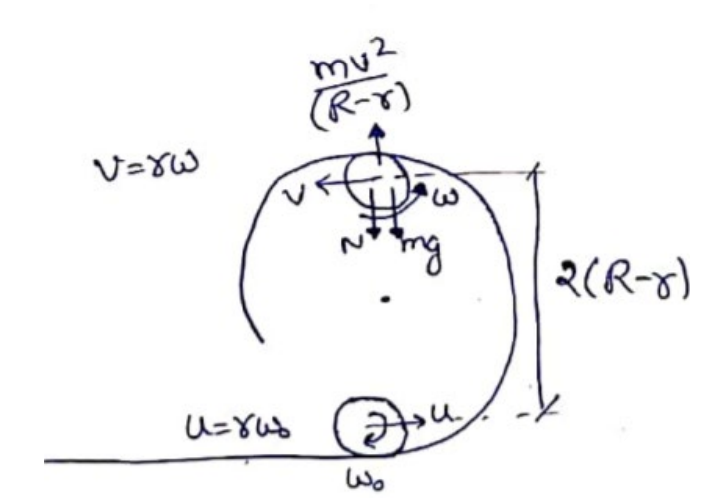
For minimum u, the ball will just be in contact with surface at top. So, $\mathrm{N}=0$
$m g=\frac{m v^{2}}{(R-r)}$
$v^{2}=g(R-r)$
Now, by energy conservation $\frac{1}{2} m u^{2}+\frac{1}{2} I \omega_{0}^{2}=\frac{1}{2} m v^{2}+\frac{1}{2} I \omega^{2}+m g \cdot 2(R-r)$
$\frac{1}{2} m u^{2}+\frac{1}{2}\left(\frac{2}{5} m r^{2}\right)\left(\frac{u^{2}}{r^{2}}\right)=\frac{1}{2} m g(R-r)+\frac{1}{2}\left(\frac{2}{5} m r^{2}\right)\left(\frac{g(R-r)}{r^{2}}\right)+2 m g(R-r)$
$u=\sqrt{\frac{27}{7} g(R-r)}$
