Question:
A solid sphere of mass $m$ is released from rest from the rim of a hemispherical cup so that it rolls along the surface. If the rim of the hemisphere is kept horizontal, find the normal force exerted by the cup on the ball when the ball reaches the bottom of the cup.
Solution:
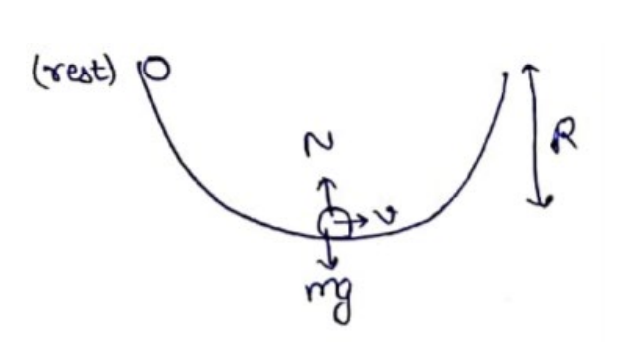
By conservation of energy
$m g R=\frac{1}{2} I \omega^{2}+\frac{1}{2} m v^{2}$
$m g R=\frac{1}{2}\left(\frac{2}{5} m R^{2}\right)\left(\frac{v^{2}}{R^{2}}\right)+\frac{1}{2} m v^{2}$
Normal contact at bottom
$N-m g=\frac{m v^{2}}{R}$
$N=m g+\frac{m}{R}\left(\frac{10}{7} g R\right)$
$N=\frac{17}{7} m g$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
