Question:
The descending pulley shown in figure has a radius $20 \mathrm{~cm}$ and moment of inertia $0.20 \mathrm{~kg}^{-} \mathrm{m}^{2}$. The fixed pulley is light and the horizontal plane frictionless. Find the acceleration of the block if its mass is $1.0 \mathrm{~kg}$.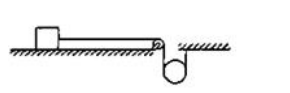
Solution:
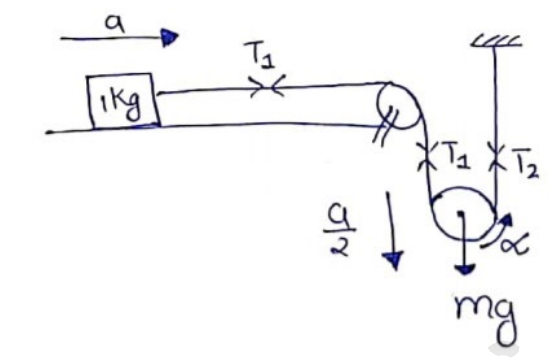
Translatory Motion Equation
$T_{1}=1, a-(\mathrm{i})$
$\mathrm{mg}-\left(T_{1}+T_{2}\right)=\mathrm{m}^{\frac{a}{2}}-(\mathrm{ii})$
Rotational Motion Equation
$\tau=\mathrm{I} \alpha$
$\operatorname{mg}-\left(T_{1}+T_{2}\right)=m^{\frac{a}{2}}-(\mathrm{ii})$
$T_{2}-T_{1}=\frac{l}{R}\left(\frac{a}{2 R}\right)_{-(\mathrm{iii})}$
$I=\frac{m R^{2}}{2}$
$(0.2)=\frac{m}{2}(0.2)^{2}$
$\mathrm{m}=10 \mathrm{~kg}$-(iv)
Using, (i),(ii),(iii) and (iv)
$a=10 \mathrm{~m} / \mathrm{s}^{2}$
