Solve the following :

a)

Applied force must be greater than net force which is acting downwards to make to move up. $F_{\text {req }}=\mu \mathrm{N}+\mathrm{mg} \sin 30^{\circ}$

$\mathrm{N}=\mathrm{mg} \cos 30^{\circ}$

$M=2 k g, g=9.8 \mathrm{~m} / \mathrm{s}^{2}, \mu=0.2$

On substituting, $F_{\text {req }}=13 \mathrm{~N}$.

b)

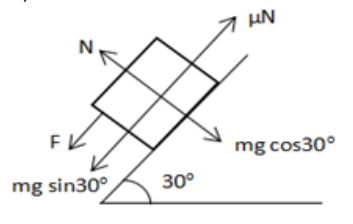
Net force acting down the incline is given by

$F_{\text {net }}=2 g \sin 30^{\circ}-\mu \mathrm{N}$

$=2 \times 9.8 \times 1 / 2-(0.2)\left[m g \cos 30^{\circ}\right]$

$=9.8-0.2[2 \times 9.8 \times \sqrt{3 / 2}]$

$=6.41 \mathrm{~N}$

$6.41$ is the force acting down the inclined plane.

This is enough for the body to slide down. No need to exert extra force. So, force required is zero.