Solve the following pairs of equations

(i) Given pair of linear equations are is

$x+y=3.3$ $\ldots($ (i)

and $\frac{0.6}{3 x-2 y}=-1$

$\Rightarrow$ $0.6=-3 x+2 y$

$\Rightarrow \quad 3 x-2 y=-0.6$ ...(ii)

Now, multiplying Eq. (i) by 2 and then adding with Eq. (ii), we get

$\Rightarrow \quad 2 x+2 y=6.6$

$\Rightarrow \quad 3 x-2 y=-0.6$

$5 x=6 \Rightarrow x=\frac{6}{5}=1.2$

Now, put the value of $x$ in Eq. (i), we get

$1.2+y=3.3$

$\Rightarrow \quad y=3.3-1.2$

$\Rightarrow \quad y=2.1$

Hence, the required values of $x$ and $y$ are $1.2$ and $2.1$, respectively.

(ii) Given, pair of linear equations is

$\frac{x}{3}+\frac{y}{4}=4$  $\ldots$ (i)

and $\quad \frac{5 x}{6}-\frac{y}{8}=4$

On multiplying both sides by LCM $(6,8)=24$, we get

$20 x-3 y=96$ ... (ii)

Now, adding Eqs. (i) and (ii), we get

$24 x=144$

$\Rightarrow \quad x=6$

Now, put the value of $x$ in Eq. (i), we get

$4 \times 6+3 y=48$

$\Rightarrow \quad 3 y=48-24$

$\Rightarrow \quad 3 y=24 \Rightarrow y=8$

Hence, the required values of $x$ and $y$ are 6 and 8 , respectively.

(iii) Given pair of linear equations are

$4 x+\frac{6}{y}=15$ $\ldots(\mathrm{i})$

 and   $6 x-\frac{8}{y}=14, y \neq 0$ ...(ii)

Let $u=\frac{1}{y}$, then above equation becomes

$4 x+6 u=15$  ..(iii)

 and $\quad 6 x-8 u=14$ $6 x-8 u=14$ $\ldots$.(iv)

On multiplying Eq. (iii) by 8 and Eq. (iv) by 6 and then adding both of them, we get

$32 x+48 u=120$

$36 x-48 u=84 \Rightarrow 68 x=204$

$\Rightarrow \quad x=3$

Now, put the value of $x$ in Eq. (iii), we get

$4 \times 3+6 u=15$

$\Rightarrow \quad 6 u=15-12 \Rightarrow 6 u=3$

$\Rightarrow \quad u=\frac{1}{2} \Rightarrow \frac{1}{y}=\frac{1}{2}$ $\left[\because u=\frac{1}{y}\right]$

$\Rightarrow \quad y=2$

Hence, the required values of $x$ and $y$ are 3 and 2, respectively.

(iv) Given pair of linear equations is

$\frac{1}{2 x}-\frac{1}{y}=-1$ $\ldots$ (i)

and $\frac{1}{x}+\frac{1}{2 y}=8, x, y \neq 0$ ....(ii)

Let $u=\frac{1}{x}$ and $v=\frac{1}{y}$, then the above equations becomes

$\frac{u}{2}-v=-1$

$\Rightarrow \quad u-2 v=-2 \quad$...(iii)

and $u+\frac{v}{2}=8$

$\Rightarrow$ $2 u+v=16$ ...(iv)

On, multiplying Eq. (iv) by 2 and then adding with Eq. (iii), we get

$4 u+2 v=32$

$\frac{u-2 v=-2}{5 u=30}$

$\Rightarrow \quad u=6$

Now, put the value of $u$ in Eq. (iv), we get

$2 \times 6+v=16$

$\Rightarrow \quad v=16-12=4$

$\Rightarrow \quad v=4$

$\therefore$ $x=\frac{1}{u}=\frac{1}{6}$ and $y=\frac{1}{v}=\frac{1}{4}$

Hence, the required values of $x$ and $y$ are $\frac{1}{6}$ and $\frac{1}{4}$, respectively.

(v) Given pair of linear equations is 

$43 x+67 y=-24$   ...(i)

and $67 x+43 y=24$ $\ldots$ (ii)

On multiplying Eq. (i) by 43 and Eq. (ii) by 67 and then subtracting both of them, we get

$(67)^{2} x+43 \times 67 y=24 \times 67$

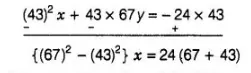
$\Rightarrow \quad(67+43)(67-43) x=24 \times 110 \quad\left[\because\left(a^{2}-b^{2}\right)=(a-b)(a+b)\right]$

$\Rightarrow \quad 110 \times 24 x=24 \times 110$

$\Rightarrow \quad x=1$

Now, put the value of $x$ in Eq. (i), we get

$43 \times 1+67 y=-24$

$\Rightarrow \quad 67 y=-24-43$

$\Rightarrow \quad .67 y=-67$

$\Rightarrow \quad y=-1$

Hence, the required values of $x$ and $y$ are 1 and $-1$, respectively.

(vi) Given pair of linear equations is 

$\frac{x}{a}+\frac{y}{b}=a+b$ $\ldots$ (i)

and $\frac{x}{a^{2}}+\frac{y}{b^{2}}=2, a, b \neq 0$  ..(ii)

On multiplying Eq. (i) by $\frac{1}{a}$ and then subtracting from Eq. (ii), we get

$\frac{x}{a^{2}}+\frac{y}{b^{2}}=2$

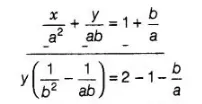
$\Rightarrow \quad y\left(\frac{a-b}{a b^{2}}\right)=1-\frac{b}{a}=\left(\frac{a-b}{a}\right)$

$\Rightarrow \quad y=\frac{a b^{2}}{a} \Rightarrow y=b^{2}$

Now, put the value of $y$ in Eq. (ii), we get

$\frac{x}{a^{2}}+\frac{b^{2}}{b^{2}}=2$

$\Rightarrow \quad \frac{x}{a^{2}}=2-1=1$

$\Rightarrow \quad x=a^{2}$

Hence, the required values of $x$ and $y$ are $a^{2}$ and $b^{2}$, respectively.

(vii) Given pair of equations is

$\frac{2 x y}{x+y}=\frac{3}{2}$, where $x+y \neq 0$

$\Rightarrow \quad \frac{x+y}{2 x y}=\frac{2}{3}$

$\Rightarrow \quad \frac{x}{x y}+\frac{y}{x y}=\frac{4}{3}$

$\Rightarrow \quad \frac{1}{y}+\frac{1}{x}=\frac{4}{3}$ ...(i)

and $\frac{x y}{2 x-y}=\frac{-3}{10}$, where $2 x-y \neq 0$

$\Rightarrow \quad \frac{2 x-y}{x y}=\frac{-10}{3}$

$\Rightarrow \quad \frac{2 x}{x y}-\frac{y}{x y}=\frac{-10}{3}$

$\Rightarrow \quad \frac{2}{y}-\frac{1}{x}=\frac{-10}{3}$ .....(ii)

Now, put $\frac{1}{x}=u$ and $\frac{1}{y}=v$, then the pair of equations becomes

$v+u=\frac{4}{3}$ ......(iii)

and $2 v-u=\frac{-10}{3}$ .....(iv)

On adding both equations, we get

$3 v=\frac{4}{3}-\frac{10}{3}=\frac{-6}{3}$

$\Rightarrow \quad 3 v=-2$

$\Rightarrow \quad v=\frac{-2}{3}$

Now, put the value of $v$ in Eq. (iii), we get

$\frac{-2}{3}+u=\frac{4}{3}$

$\Rightarrow \quad u=\frac{4}{3}+\frac{2}{3}=\frac{6}{3}=2$

$\therefore$ $x=\frac{1}{u}=\frac{1}{2}$

and $y=\frac{1}{v}=\frac{1}{(-2 / 3)}=\frac{-3}{2}$

Hence, the required values of $x$ and $y$ are $\frac{1}{2}$ and $\frac{-3}{2}$, respectively.