Let $\mathrm{f}:[-1,1] \rightarrow \mathrm{R}$ be defined as $\mathrm{f}(\mathrm{x})=\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}$ for all $x \in[-1,1]$, where $a, b, c \in R$ such that $f(-1)=2, f^{\prime}(-1)=1$ and for $x \in(-1,1)$ the maximum value of $\mathrm{f}^{\prime \prime}(\mathrm{x})$ is $\frac{1}{2}$. If $\mathrm{f}(\mathrm{x}) \leq \alpha$, $x \in[-1,1]$, then the least value of $\alpha$ is equal to
$f:[-1,1] \rightarrow R$
$f(x)=a x^{2}+b x+c$
$f(-1)=a-b+c=2$..(1)
$f^{\prime}(-1)=-2 a+b=1$..(2)
$f^{\prime \prime}(x)=2 a$
$\Rightarrow$ Max. value of $f^{\prime \prime}(x)=2 a=\frac{1}{2}$
$\Rightarrow \mathrm{a}=\frac{1}{4} ; \quad \mathrm{b}=\frac{3}{2} ; \quad \mathrm{c}=\frac{13}{4}$
$\therefore \quad f(x)=\frac{x^{2}}{4}+\frac{3}{2} x+\frac{13}{4}$
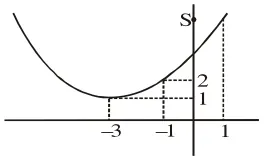
For, $x \in[-1,1] \Rightarrow 2 \leq f(x) \leq 5$
$\therefore \quad$ Least value of $\alpha$ is 5
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.