Question:
Let $A(a, 0), B(b, 2 b+1)$ and $C(0, b), b \neq 0,|b| \neq 1$, be points such that the area of triangle $A B C$ is 1 sq. unit, then the sum of all possible values of a is :
Correct Option: , 4
Solution:
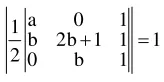
$\Rightarrow\left|\begin{array}{ccc}\mathrm{a} & 0 & 1 \\ \mathrm{~b} & 2 \mathrm{~b}+1 & 1 \\ 0 & \mathrm{~b} & 1\end{array}\right|=\pm 2$
$\Rightarrow a(2 b+1-b)-0+1\left(b^{2}-0\right)=\pm 2$
$\Rightarrow a=\frac{\pm 2-b^{2}}{b+1}$
$\therefore \mathrm{a}=\frac{2-\mathrm{b}^{2}}{\mathrm{~b}+1}$ and $\mathrm{a}=\frac{-2-\mathrm{b}^{2}}{\mathrm{~b}+1}$
sum of possible values of 'a' is
$=\frac{-2 b^{2}}{a+1}$ Ans
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.