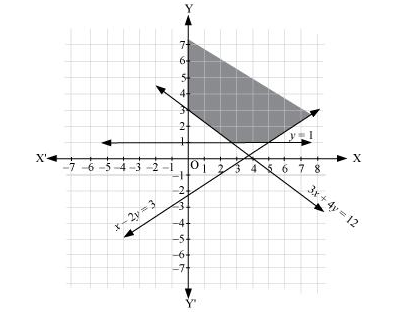
Solve the following system of inequalities graphically:

$x-2 y \leq 3 \ldots(1)$

$3 x+4 y \geq 12 \ldots(2)$

$y \geq 1 \ldots(3)$

The graph of the lines, x – 2y = 3, 3x + 4y = 12, and y = 1, are drawn in the figure below.

Inequality (1) represents the region above the line, x – 2y = 3 (including the line x – 2y = 3). Inequality (2) represents the region above the line, 3x + 4y = 12 (including the line 3x + 4y = 12). Inequality (3) represents the region above the line, y = 1 (including the line y = 1).

The inequality, x ≥ 0, represents the region on the right hand side of y-axis (including y-axis).

Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on the respective lines and y- axis as follows.