Solve the following systems of equations:

The given equations are:

$\frac{3}{x+y}+\frac{2}{x-y}=2$

$\frac{9}{x+y}-\frac{4}{x-y}=1$

Let $\frac{1}{x+y}=u$ and $\frac{1}{x-y}=v$ then equations are

$3 u+2 v=2 \ldots(i)$

$9 u-4 v=1 \ldots(i i)$

Multiply equation $(i)$ by 2 and add both equations, we get

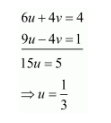
Put the value of $u$ in equation $(i)$, we get

$3 \times \frac{1}{3}+2 v=2$

$\Rightarrow 2 v=1$

$\Rightarrow v=\frac{1}{2}$

Then

$\frac{1}{x+y}=\frac{1}{3}$

$\Rightarrow x+y=3$

Add both equations, we get

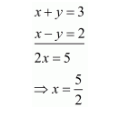
Put the value of $x$ in first equation, we get

$\frac{5}{2}+y=3$

$\Rightarrow y=\frac{1}{2}$

Hence the value of $x=\frac{5}{2}$ and $y=\frac{1}{2}$.