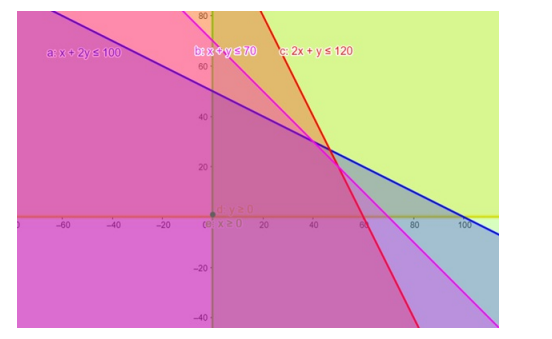
Solve the given inequalities

The graphical representation of $x+2 y \leq 100,2 x+y \leq 120$

$x+y \leq 70, y \geq 0, x \geq 0$ is given by common region in the figure below.

$x+2 y \leq 100 \ldots \ldots$ (1)

$2 x+y \leq 120 \ldots \ldots$ (2)

$x \geq 0 \ldots \ldots$ (3)

$y \geq 0 \ldots \ldots$ (4)

$x+y \leq 70 \ldots \ldots$ (5)

Inequality (1) represents the region below line $x+2 y=100$ (including the line $x+2 y=100$ ).

Inequality (2) represents the region below line $2 x+y=120$ (including the line $2 x+y=120$ ).

Inequality (3) represents the region in front of line $x=0$ (including the line $x=0$ ).

Inequality (4) represents the region above line $y=0$ (including the line $y=0$ ).

Inequality (5) represents the region below line $x+y=70$ (including the line $x+y=70$ )

Therefore,every point in the common shaded region including the points on the respective lines represents the solution for the given inequalities.

This can be represented as follows,