Question:
Solve the given inequality and show the graph of the solution on number line: $\frac{x}{2} \geq \frac{(5 x-2)}{3}-\frac{(7 x-3)}{5}$
Solution:
$\frac{x}{2} \geq \frac{(5 x-2)}{3}-\frac{(7 x-3)}{5}$
$\Rightarrow \frac{x}{2} \geq \frac{5(5 x-2)-3(7 x-3)}{15}$
$\Rightarrow \frac{x}{2} \geq \frac{25 x-10-21 x+9}{15}$
$\Rightarrow \frac{x}{2} \geq \frac{4 x-1}{15}$$\Rightarrow 15 x \geq 2(4 x-1)$
$\Rightarrow 15 x \geq 8 x-2$
$\Rightarrow 15 x-8 x \geq 8 x-2-8 x$
$\Rightarrow 7 x \geq-2$
$\Rightarrow x \geq-\frac{2}{7}$
The graphical representation of the solutions of the given inequality is as follows.
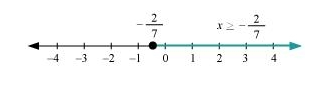
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
