Question:
If $A=\{x: x \in R, x<5\}$ and $B=\{x: x \in R, x>4\}$, find $A \cap B$.
Solution:
$A=\{x: x \in R, x<5\}$
As $x$ takes all real values upto 5 hence the set $A$ will contain all numbers from $-\infty$ to 5
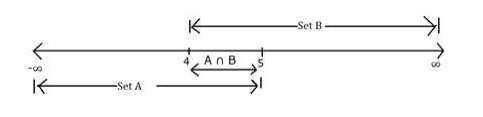
$A=(-\infty, 5)$
$B=\{x: x \in R, x>4\}$
As $x$ takes all real values greater than 4 hence the set $B$ will contain values from 4 to $\infty$
$B=(4,-\infty)$
Hence their intersection or the common part between sets $A$ and $B$ would be values from 4 to 5
Hence $A \cap B=(4,5)$
Representing the sets on number line
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
