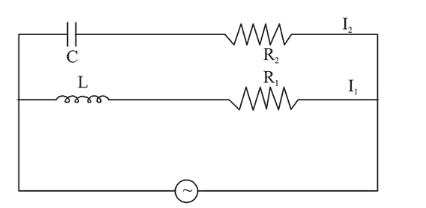
In the above circuit, $\mathrm{C}=\frac{\sqrt{3}}{2} \mu \mathrm{F}, \mathrm{R}_{2}=20 \Omega, \mathrm{L}=\frac{\sqrt{3}}{10} \mathrm{H}$ and
$\mathrm{R}_{1}=10 \Omega$. Current in $\mathrm{L}-\mathrm{R}_{1}$ path is $\mathrm{I}_{1}$ and in $\mathrm{C}-\mathrm{R}_{2}$ path it is $\mathrm{I}_{2}$.
The voltage of A.C source is given by, $\mathrm{V}=200 \sqrt{2} \sin (100 \mathrm{t})$ volts. The phase difference between $\mathrm{I}_{1}$ and $\mathrm{I}_{2}$ is :
Correct Option: , 4
(4)
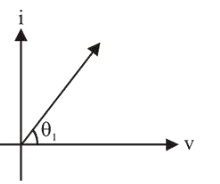
Capacitive reactance,
$X_{c}=\frac{1}{\omega \mathrm{C}}=\frac{4}{10^{-6} \times \sqrt{3} \times 100}=\frac{2 \times 10^{4}}{\sqrt{3}}$
$\tan \theta_{1}=\frac{X_{C}}{R_{2}}=\frac{10^{3}}{\sqrt{3}}$
$\theta_{1}$ is close to $90^{\circ}$
For L-R circuit
$X_{L}=\omega L=100 \times \frac{\sqrt{3}}{10}=10 \sqrt{3}$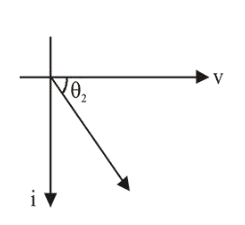
$R_{1}=10$
$\tan \theta_{2}=\frac{X_{L}}{R_{1}}$
$\tan \theta_{2}=\sqrt{3} \quad \Rightarrow \quad \theta_{2}=\tan ^{-1}(\sqrt{3})$]
$\theta_{2}=60^{\circ}$
So,
phase difference comes out $90^{\circ}+60^{\circ}=150^{\circ}$ If $R_{2}$ is $20 \mathrm{~K} \Omega$
then phase difference comes out to be $60+30=90^{\circ}$.
