Solve this

Given :

$\left(\frac{4 x-3}{2 x+1}\right)-10\left(\frac{2 x+1}{4 x-3}\right)=3$

Putting $\frac{4 x-3}{2 x+1}=y$, we get:

$y-\frac{10}{y}=3$

$\Rightarrow \frac{y^{2}-10}{y}=3$

$\Rightarrow y^{2}-10=3 y[$ On cross multiplying $]$

$\Rightarrow y^{2}-3 y-10=0$

$\Rightarrow y^{2}-(5-2) y-10=0$

$\Rightarrow y^{2}-5 y+2 y-10=0$

$\Rightarrow y(y-5)+2(y-5)=0$

$\Rightarrow(y-5)(y+2)=0$

$\Rightarrow y-5=0$ or $y+2=0$

$\Rightarrow y=5$ or $y=-2$

Case I

If $y=5$, we get:

$\frac{4 x-3}{2 x+1}=5$

$\Rightarrow 4 x-3=5(2 x+1)[$ On cross multiplying $]$

$\Rightarrow 4 x-3=10 x+5$

$\Rightarrow-6 x=8$

$\Rightarrow-6 x=8$

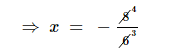
$\Rightarrow x=-\frac{4}{3}$

Case II

If $y=-2$, we get:

$\frac{4 x-3}{2 x+1}=-2$

$\Rightarrow 4 x-3=-2(2 x+1)$

$\Rightarrow 4 x-3=-4 x-2$

$\Rightarrow 8 x=1$

$\Rightarrow x=\frac{1}{8}$

Hence, the roots of the equation are $-\frac{4}{3}$ and $\frac{1}{8}$.