Question:
The function $f(x)=\left\{\begin{array}{l}\frac{\pi}{4}+\tan ^{-1} x,|x| \leq 1 \\ \frac{1}{2}(|x|-1),|x|>1\end{array}\right.$ is :
Correct Option: 1
Solution:
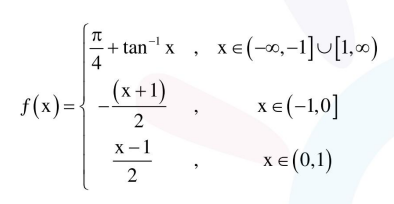
for continuity at $\mathrm{x}=-1$
L.H.L. $=\frac{\pi}{4}-\frac{\pi}{4}=0$
R.H.L. $=0$
so, continuous at $x=-1$
for continuity at $x=1$
L.H.L. $=0$
R.H.L. $=\frac{\pi}{4}+\frac{\pi}{4}=\frac{\pi}{2}$
so, not continuous at $x=1$
For differentiability at $x=-1$
L.H.D. $=\frac{1}{1+1}=\frac{1}{2}$
R.H.D. $=-\frac{1}{2}$
so, non differentiable at $x=-1$
