Let $\mathrm{E}_{1}: \frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1, \mathrm{a}>\mathrm{b}$. Let $\mathrm{E}_{2}$ be another ellipse such that it touches the end points of major axis of $E_{1}$ and the foci of $E_{2}$ are the end points of minor axis of $E_{1}$. If $E_{1}$ and $E_{2}$ have same eccentricities, then its value is :
Correct Option: 1,
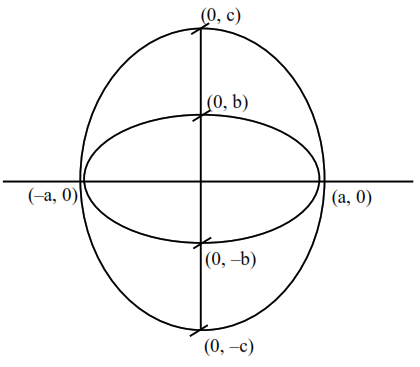
$e^{2}=1-\frac{b^{2}}{a^{2}}$
$e^{2}=1-\frac{a^{2}}{c^{2}}$
$\Rightarrow \frac{b^{2}}{a^{2}}=\frac{a^{2}}{c^{2}}$
$\Rightarrow \mathrm{c}^{2}=\frac{\mathrm{a}^{4}}{\mathrm{~b}^{2}} \Rightarrow \mathrm{c}=\frac{\mathrm{a}^{2}}{\mathrm{~b}}$
Also $b=c e$
$\Rightarrow \mathrm{c}=\frac{\mathrm{b}}{\mathrm{e}}$
$\frac{\mathrm{b}}{\mathrm{e}}=\frac{\mathrm{a}^{2}}{\mathrm{~b}}$
$\Rightarrow \mathrm{e}=\frac{\mathrm{b}^{2}}{\mathrm{a}^{2}}=1-\mathrm{e}^{2}$
$\Rightarrow \mathrm{e}^{2}+\mathrm{e}-1=0$
$\Rightarrow \mathrm{e}=\frac{-1+\sqrt{5}}{2}$
