Question:
Let $f: R \rightarrow R: f(x)=x^{2}$
Determine
(i) range (f)
(ii) $\{x: f(x)=4\}$
Solution:
Given: $f(x)=x^{2}$
The graph for the given function is
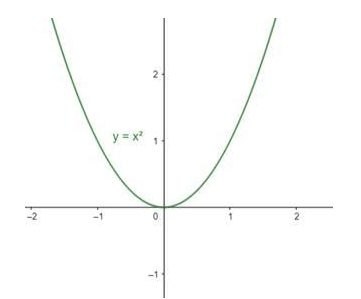
(i) Range(f):
For finding the range of the given function, let y = f(x)
Therefore,
$y=x^{2}$
$x=\sqrt{y}$
The value of $y \geq 0$.
Hence, Range(f) is $[0, \infty)$.
(ii) Let $y=f(x)=x^{2}$
Given $y=4$
Therefore, $x^{2}=4$
$x=2$ or $x=-2$
The set of values for which $y=4$ is $x=\{2,-2\}$.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
