Question:
$f(x)=x^{3}(2 x-1)^{3}$
Solution:
Given : $f(x)=x^{3}(2 x-1)^{3}$
$\Rightarrow f^{\prime}(x)=3 x^{2}(2 x-1)^{3}+6 x^{3}(2 x-1)^{2}$
For the local maxima or minima, we must have
$f^{\prime}(x)=0$
$\Rightarrow 3 x^{2}(2 x-1)^{3}+6 x^{3}(2 x-1)^{2}=0$
$\Rightarrow 3 x^{2}(2 x-1)^{2}(2 x-1+2 x)=0$
$\Rightarrow x^{2}(2 x-1)^{2}(4 x-1)=0$
$\Rightarrow x=0, \frac{1}{2}$ and $\frac{1}{4}$
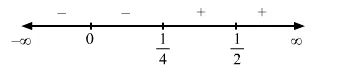
Since $f^{\prime}(x)$ changes from negative to positive when $x$ increases through $\frac{1}{4}, x=\frac{1}{4}$ is a point of local minima.
The local minimum value of $f(x)$ at $x=\frac{1}{4}$ is given by
$\left(\frac{1}{4}\right)^{3}\left(\frac{1}{2}-1\right)^{3}=\frac{-1}{512}$
