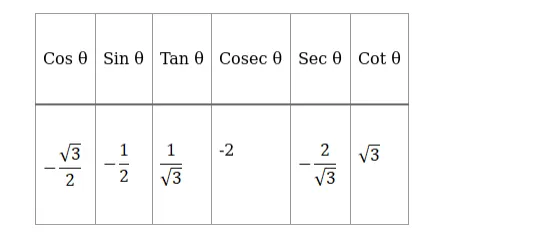
If $\cos \theta=\frac{-\sqrt{3}}{2}$ and $\theta$ lies in Quadrant III, find the value of all the other five trigonometric functions.
Given: $\cos \theta=\frac{-\sqrt{3}}{2}$
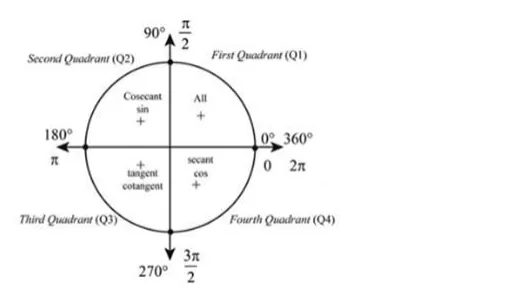
Since, θ is in IIIrd Quadrant. So, sin and cos will be negative but tan will be positive
We know that,
$\cos ^{2} \theta+\sin ^{2} \theta=1$
Putting the values, we get
$\left(-\frac{\sqrt{3}}{2}\right)^{2}+\sin ^{2} \theta=1$ [given]
$\Rightarrow \frac{3}{4}+\sin ^{2} \theta=1$
$\Rightarrow \sin ^{2} \theta=1-\frac{3}{4}$
$\Rightarrow \sin ^{2} \theta=\frac{4-3}{4}$
$\Rightarrow \sin ^{2} \theta=\frac{1}{4}$
$\Rightarrow \sin \theta=\sqrt{\frac{1}{4}}$
$\Rightarrow \sin \theta=\pm \frac{1}{2}$
Since, $\theta$ in III $^{\text {rd }}$ quadrant and $\sin \theta$ is negative in III $^{\text {rd }}$ quadrant
$\therefore \sin \theta=-\frac{1}{2}$
Now,
$\tan \theta=\frac{\sin \theta}{\cos \theta}$
Putting the values, we get
$\tan \theta=\frac{-\frac{1}{2}}{-\frac{\sqrt{3}}{2}}$
$=-\frac{1}{2} \times\left(-\frac{2}{\sqrt{3}}\right)$
$=\frac{1}{\sqrt{3}}$
Now,
$\operatorname{cosec} \theta=\frac{1}{\sin \theta}$
Putting the values, we get
$\operatorname{cosec} \theta=\frac{1}{-\frac{1}{2}}$
$=-2$
Now,
$\sec \theta=\frac{1}{\cos \theta}$
Putting the values, we get
$\sec \theta=\frac{1}{-\frac{\sqrt{3}}{2}}$
$=-\frac{2}{\sqrt{3}}$
Now,
$\cot \theta=\frac{1}{\tan \theta}$
Putting the values, we get
$\cot \theta=\frac{1}{\frac{1}{\sqrt{3}}}$
$=\sqrt{3}$
Hence, the values of other trigonometric Functions are: