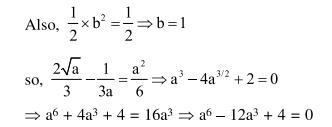Solve this following

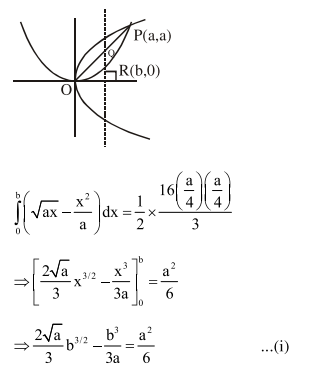
For a > 0 , let the curves $C_{1}: y^{2}=a x$ and $C_{2}: x^{2}=$ ay intersect at origin $O$ and a point $P$. Let the line $\mathrm{x}=\mathrm{b}(0<\mathrm{b}<\mathrm{a})$ intersect the chord OP and the $x$-axis at points $Q$ and $R$, respectively. If the line $x=b$ bisects the area bounded by the curves, $C_{1}$ and $C_{2}$, and the area of $\triangle \mathrm{OQR}=\frac{1}{2}$, then 'a' satisfies the equation