Question:
Let $f:(-1,1) \rightarrow R$ be a function defined by
$f(x)=\max \left\{-|x|,-\sqrt{1-x^{2}}\right\} .$ If $K$ be the set of
all points at which $f$ is not differentiable, then $\mathrm{K}$ has exactly :
Correct Option: 1
Solution:
$\mathrm{f}:(-1,1) \rightarrow \mathrm{R}$
$f(x)=\max \left\{-|x|,-\sqrt{1-x^{2}}\right\}$
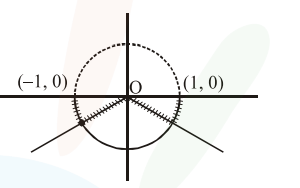
Non-derivable at 3 points in $(-1,1)$
Option (1)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
