If $P$ is a point on the parabola $y=x^{2}+4$ which is closest to the straight line $y=4 x-1$, then the co-ordinates of $\mathrm{P}$ are :
Correct Option: , 4
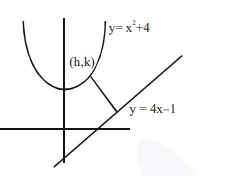
$P: y=x^{2}+4$
$\mathrm{k}=\mathrm{h}^{2}+4$
$\mathrm{L}: \mathrm{y}=4 \mathrm{x}-1$
$y-4 x+1=0$
$\mathrm{d}=\mathrm{AB}=\left|\frac{\mathrm{k}-4 \mathrm{~h}+1}{\sqrt{5}}\right|=\left|\frac{\mathrm{h}^{2}-4-4 \mathrm{~h}+1}{\sqrt{5}}\right|$
$\frac{\mathrm{d}(\mathrm{d})}{\mathrm{dh}}=\frac{2 \mathrm{~h}-4}{\sqrt{5}}=0$
$h=2$
$\frac{\mathrm{d}^{2}(\mathrm{~d})}{\mathrm{dh}^{2}}=\frac{2}{\sqrt{5}}>0$
$\begin{array}{ll}\therefore & \mathrm{k}=4+4=8 \\ \therefore & \text { Point }(2,8)\end{array}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.