Solve this following

Question:
Two sides of a parallelogram are along the lines, $x+y=3$ and $x-y+3=0$. If its diagonals intersect at $(2,4)$, then one of its vertex is :

Correct Option: , 4

Solution:

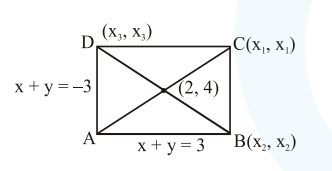
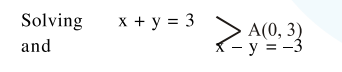
$\frac{x_{1}+0}{2}=2 ; \quad x_{i}=4 \quad$ similarly $\quad y_{1}=5$

$\mathrm{C} \Rightarrow(4,5)$

Now equation of $B C$ is $x-y=-1$

and equation of CD is $x+y=9$

Solving $x+y=9$ and $x-y=-3$

Point $\mathrm{D}$ is $(3,6)$

Option (4)