Question:
Let $f(x)= \begin{cases}\max \left\{|x|, x^{2}\right\}, & |x| \leq 2 \\ 8-2|x|, & 2 Let $S$ be the set of points in the interval $(-4,4)$ at which $\mathrm{f}$ is not differentiable. Then $S$ :
Correct Option: , 3
Solution:
$f(x)= \begin{cases}8+2 x, & -4 \leq x<-2 \\ x^{2}, & -2 \leq x \leq-1 \\ |x|, & -1 $f(x)$ is not differentiable at $x=\{-2,-1,0,1,2\}$ $\Rightarrow S=\{-2,-1,0,1,2\}$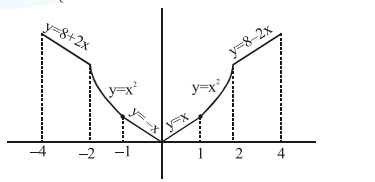
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
