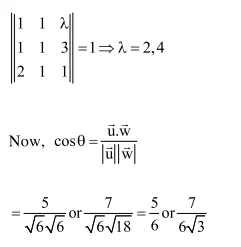Question:
Let the volume of a parallelopiped whose coterminous edges are given by $\overrightarrow{\mathrm{u}}=\hat{\mathrm{i}}+\hat{\mathrm{j}}+\lambda \hat{\mathrm{k}}, \overrightarrow{\mathrm{v}}=\hat{\mathrm{i}}+\hat{\mathrm{j}}+3 \hat{\mathrm{k}}$ and $\overrightarrow{\mathrm{w}}=2 \hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}}$ be $1 \mathrm{cu}$. unit. If $\theta$ be the angle between the edges $\overrightarrow{\mathrm{u}}$ and $\overrightarrow{\mathrm{w}}$, then $\cos \theta$ can be
Correct Option: 1
Solution: