Question:
Let $f: \mathbb{R}-\{3\} \rightarrow \mathrm{R}-\{1\}$ be defined by
$f(\mathrm{x})=\frac{\mathrm{x}-2}{\mathrm{x}-3}$. Let $\mathrm{g}: \mathrm{R} \rightarrow \mathrm{R}$ be given as
$g(x)=2 x-3$. Then, the sum of all the values
of $x$ for which $f^{-1}(x)+g^{-1}(x)=\frac{13}{2}$ is equal to
Correct Option: , 3
Solution:
$f(x)=y=\frac{x-2}{x-3}$
$\therefore x=\frac{3 y-2}{y-1}$
$\therefore f^{-1}(x)=\frac{3 x-2}{x-1}$
$\& g(x)=y=2 x-3$
$\therefore x=\frac{y+3}{2}$
$\therefore g^{-1}(x)=\frac{x+3}{2}$
$\because f^{-1}(x)+g^{-1}(x)=\frac{13}{2}$
$\therefore x^{2}-5 x+6$
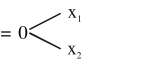
$\therefore$ sum of roots
$x_{1}+x_{2}=5$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.