Question:
A particle of charge $\mathrm{q}$ and mass $\mathrm{m}$ is moving with a velocity $-v \hat{i}(v \neq 0)$ towards a large screen placed in the Y-Z plane at a distance $d$. If there is a magnetic field $\overrightarrow{\mathrm{B}}=\mathrm{B}_{0} \hat{\mathrm{k}}$, the minimum value of $v$ for which the particle will not hit the screen is:
Correct Option: , 2
Solution:
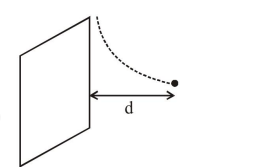
In uniform magnetic field particle moves in a circular path, if the radius of the circular path is 'd', particle will not hit the screen.
$\mathrm{d}=\frac{\mathrm{mv}}{\mathrm{qB}_{0}}$
$v=\frac{q B_{0} d}{m}$
$\therefore$ correct option is (2)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
