Students of a school are standing in rows

Solution:

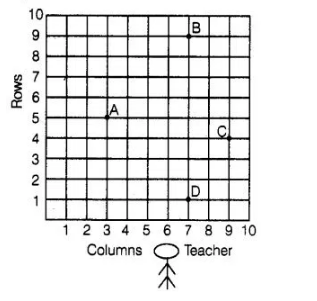
Yes, from the figure we observe that the positions of four students A, B, C and D are (3, 5), (7, 9), (11, 5) and (7,1) respectively i.e., these are four

vertices of a quadrilateral. Now, we will find the type of this quadrilateral. For this, we will find all its sides.

We see that, AB = BC = CD = DA i.e., all sides are equal.

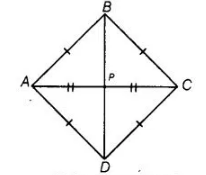
Now, $A B=\sqrt{(7-3)^{2}+(9-5)^{2}}$

by distance formula, $\left.d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\right]$

$A B=\sqrt{(4)^{2}+(4)^{2}}=\sqrt{16+16}$

$A B=4 \sqrt{2}$

$B C=\sqrt{(11-7)^{2}+(5-9)^{2}}=\sqrt{(4)^{2}+(-4)^{2}}$

$=\sqrt{16+16}=4 \sqrt{2}$

$C D=\sqrt{(7-11)^{2}+(1-5)^{2}}=\sqrt{(-4)^{2}+(-4)^{2}}$

$=\sqrt{16+16}=4 \sqrt{2}$

and $D A=\sqrt{(3-7)^{2}+(5-1)^{2}}=\sqrt{(-4)^{2}+(4)^{2}}$

$=\sqrt{16+16}=4 \sqrt{2}$

Now, we find length of both diagonals.

$A C=\sqrt{(11-3)^{2}+(5-5)^{2}}=\sqrt{(8)^{2}+0}=8$

and $B D=\sqrt{(7-7)^{2}+(1-9)^{2}}=\sqrt{0+(-8)^{2}}=8$

Here. $\quad A C=B D$

Since, $\quad A B=B C=C D=D A$ and $A C=B D$

Which represent a square. Also known the diagonals of a square bisect each other. So, $P$ be position of Jaspal in which he is equidistant from each of the four students $A, B, C$ and $D$. $\therefore$ Coordinates of point $P \equiv$ Mid-point of $A C$

$=\left(\frac{3+11}{2}, \frac{5+5}{2}\right) \equiv\left(\frac{14}{2}, \frac{10}{2}\right)=(7,5)$

$=\left[\right.$ since, mid-point of a line segment having points $\left(x_{1}, y_{1}\right)$ and $\left.\left(x_{2}, y_{2}\right)=\left(\frac{x_{1}+y_{1}}{2}, \frac{x_{2}+y_{2}}{2}\right)\right]$

Hence, the required position of Jaspal is (7, 5).