Susan invested certain amount of money in two schemes A and B, which offer interest at the rate of 8% per annum and 9% per annum, respectively.
She received ₹ 1860 as annual interest. However, had she interchanged the amount of investments in the two schemes, she would have received ₹ 20
more as annual interest. How much money did she invest in each scheme?
Let the amount of investments in schemes A and 6 be ₹ x and ₹ y, respectively.
Case I Interest at the rate of 8% per annum on scheme A+ Interest at the rate of 9% per
annum on scheme 6 = Total amount received
$\Rightarrow \quad \frac{x \times 8 \times 1}{100}+\frac{y \times 9 \times 1}{100}=₹ 1860 \quad\left[\because\right.$ simple interest $\left.=\frac{\text { principal } \times \text { rate } \times \text { time }}{100}\right]$
$\Rightarrow \quad 8 x+9 y=186000$ ...(i)
Case II Interest at the rate of $9 \%$ per annum on scheme $A+$ Interest at the rate of $8 \%$ per
annum on scheme $B=₹ 20$ more as annual interest
$\Rightarrow \quad \frac{x \times 9 \times 1}{100}+\frac{y \times 8 \times 1}{100}=₹ 20+₹ 1860$
$\Rightarrow \quad \frac{9 x}{100}+\frac{8 y}{100}=1880$
$\Rightarrow \quad 9 x+8 y=188000$ $\ldots$ (ii)
On multiplying Eq. (i) by 9 and Eq. (ii) by 8 and then subtracting them, we get
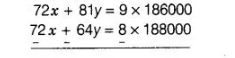
$\Rightarrow \quad 17 y=1000[(9 \times 186)-(8 \times 188)]$
$=1000(1674-1504)=1000 \times 170$
$17 y=170000 \Rightarrow y=10000$
On putting the value of $y$ in Eq. (i), we get
$8 x+9 \times 10000=186000$
$\Rightarrow \quad 8 x=186000-90000$
$\Rightarrow \quad 8 x=96000$
$\Rightarrow \quad x=12000$
On putting the value of $y$ in Eq. (i), we get
$8 x+9 \times 10000=186000$
$\Rightarrow \quad 8 x=186000-90000$
$\Rightarrow \quad 8 x=96000$
$\Rightarrow \quad x=12000$