Question.
$\tan x=-\frac{4}{3}, x$ in quadrant II
$\tan x=-\frac{4}{3}, x$ in quadrant II
solution:
Here, x is in quadrant II.
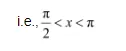
$\Rightarrow \frac{\pi}{4}<\frac{x}{2}<\frac{\pi}{2}$
Therefore, $\sin \frac{x}{2}, \cos \frac{x}{2}$ and $\tan \frac{x}{2}$ are all positive.
It is given that $\tan x=-\frac{4}{3}$.
$\sec ^{2} x=1+\tan ^{2} x=1+\left(\frac{-4}{3}\right)^{2}=1+\frac{16}{9}=\frac{25}{9}$
$\therefore \cos ^{2} x=\frac{9}{25}$
$\Rightarrow \cos x=\pm \frac{3}{5}$
As $x$ is in quadrant II, $\cos x$ is negative.
$\therefore \cos x=\frac{-3}{5}$
Now, $\cos x=2 \cos ^{2} \frac{x}{2}-1$
$\Rightarrow \frac{-3}{5}=2 \cos ^{2} \frac{x}{2}-1$
$\Rightarrow 2 \cos ^{2} \frac{x}{2}=1-\frac{3}{5}$
$\Rightarrow \cos ^{2} \frac{x}{2}=\frac{1}{5}$
$\Rightarrow \cos \frac{x}{2}=\frac{1}{\sqrt{5}} \quad\left[\because \cos \frac{x}{2}\right.$ is positive $]$
$\therefore \cos \frac{x}{2}=\frac{\sqrt{5}}{5}$
$\sin ^{2} \frac{x}{2}+\cos ^{2} \frac{x}{2}=1$
$\Rightarrow \sin ^{2} \frac{x}{2}+\left(\frac{1}{\sqrt{5}}\right)^{2}=1$
$\Rightarrow \sin ^{2} \frac{x}{2}=1-\frac{1}{5}=\frac{4}{5}$
$\Rightarrow \sin \frac{x}{2}=\frac{2}{\sqrt{5}} \quad\left[\because \sin \frac{x}{2}\right.$ is positive $]$
$\therefore \sin \frac{x}{2}=\frac{2 \sqrt{5}}{5}$
$\tan \frac{x}{2}=\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}}=\frac{\left(\frac{2}{\sqrt{5}}\right)}{\left(\frac{1}{\sqrt{5}}\right)}=2$
Thus, the respective values of $\sin \frac{x}{2}, \cos \frac{x}{2}$ and $\tan \frac{x}{2}$ are $\frac{2 \sqrt{5}}{5}, \frac{\sqrt{5}}{5}$, and 2 .
Here, x is in quadrant II.
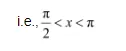
$\Rightarrow \frac{\pi}{4}<\frac{x}{2}<\frac{\pi}{2}$
Therefore, $\sin \frac{x}{2}, \cos \frac{x}{2}$ and $\tan \frac{x}{2}$ are all positive.
It is given that $\tan x=-\frac{4}{3}$.
$\sec ^{2} x=1+\tan ^{2} x=1+\left(\frac{-4}{3}\right)^{2}=1+\frac{16}{9}=\frac{25}{9}$
$\therefore \cos ^{2} x=\frac{9}{25}$
$\Rightarrow \cos x=\pm \frac{3}{5}$
As $x$ is in quadrant II, $\cos x$ is negative.
$\therefore \cos x=\frac{-3}{5}$
Now, $\cos x=2 \cos ^{2} \frac{x}{2}-1$
$\Rightarrow \frac{-3}{5}=2 \cos ^{2} \frac{x}{2}-1$
$\Rightarrow 2 \cos ^{2} \frac{x}{2}=1-\frac{3}{5}$
$\Rightarrow \cos ^{2} \frac{x}{2}=\frac{1}{5}$
$\Rightarrow \cos \frac{x}{2}=\frac{1}{\sqrt{5}} \quad\left[\because \cos \frac{x}{2}\right.$ is positive $]$
$\therefore \cos \frac{x}{2}=\frac{\sqrt{5}}{5}$
$\sin ^{2} \frac{x}{2}+\cos ^{2} \frac{x}{2}=1$
$\Rightarrow \sin ^{2} \frac{x}{2}+\left(\frac{1}{\sqrt{5}}\right)^{2}=1$
$\Rightarrow \sin ^{2} \frac{x}{2}=1-\frac{1}{5}=\frac{4}{5}$
$\Rightarrow \sin \frac{x}{2}=\frac{2}{\sqrt{5}} \quad\left[\because \sin \frac{x}{2}\right.$ is positive $]$
$\therefore \sin \frac{x}{2}=\frac{2 \sqrt{5}}{5}$
$\tan \frac{x}{2}=\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}}=\frac{\left(\frac{2}{\sqrt{5}}\right)}{\left(\frac{1}{\sqrt{5}}\right)}=2$
Thus, the respective values of $\sin \frac{x}{2}, \cos \frac{x}{2}$ and $\tan \frac{x}{2}$ are $\frac{2 \sqrt{5}}{5}, \frac{\sqrt{5}}{5}$, and 2 .
