Question:
The acceleration due to gravity on the earth's surface at the poles is $\mathrm{g}$ and angular velocity of the earth about the axis passing through the pole is $\omega$. An object is weighed at the equator and at a height $\mathrm{h}$ above the poles by using a spring balance. If the weights are found to be same, then $h$ is : ( $h<
Correct Option: , 4
Solution:
$g_{e}=g-R \omega^{2}$
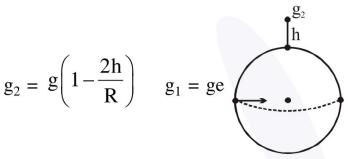
$\mathrm{g}_{2}=\mathrm{g}-\frac{2 \mathrm{gh}}{\mathrm{R}}$
Now $R \omega^{2}=\frac{2 g h}{R}$
$\mathrm{h}=\frac{\mathrm{R}^{2} \omega^{2}}{2 \mathrm{~g}}$