The altitude of a right triangle is 7 cm less than its base.

Solution:

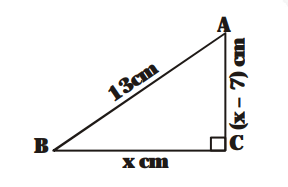
In $\triangle \mathrm{ABC}$, base $\mathrm{BC}=\mathrm{x} \mathrm{cm}$

and altitude $A C=(x-7) \mathrm{cm}$

$\angle \mathrm{ACB}=90^{\circ}$

$\mathrm{AB}=13 \mathrm{~cm}$

By Pythagoras theorem, we have



$\mathrm{BC}^{2}+\mathrm{AC}^{2}=\mathrm{AB}^{2}$

$\Rightarrow x^{2}+(x-7)^{2}=13^{2}$

$\Rightarrow x^{2}+x^{2}-14 x+49=169$

$\Rightarrow 2 x^{2}-14 x-120=0$

$\Rightarrow x^{2}-7 x-60=0$

$\Rightarrow x^{2}-12 x+5 x-60=0$

$\Rightarrow x(x-12)+5(x-12)=0$

$\Rightarrow(x+5)(x-12)=0$

$\Rightarrow x=-5$ or $x=12$

We reject $x=-5$

$\Rightarrow x=12$

Therefore, $\mathrm{BC}=12 \mathrm{~cm}$ and $\mathrm{AC}=5 \mathrm{~cm}$.