The angle of elevation of the top of a hill from a point on the horizontal plane passing through the foot of the hill is found to be $45^{\circ}$. After walking a distance of 80 meters towards the top, up a slope inclined at an angle of $30^{\circ}$ to the horizontal plane, the angle of elevation of the top of the hill becomes $75^{\circ}$. Then the height of the hill (in meters) is_____________.
Let height $(A B)=h \mathrm{~m}, C D=x \mathrm{~m}$ and $E D=y \mathrm{~m}$
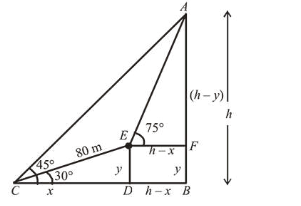
In rt. $\Delta C D E$,
$\sin 30^{\circ}=\frac{y}{80} \Rightarrow y=40$
$\cos 30^{\circ}=\frac{x}{80} \Rightarrow x=40 \sqrt{3}$
Now, in $\triangle A E F$,
$\tan 75^{\circ}=\frac{h-y}{h-x}$
$\Rightarrow(2+\sqrt{3})=\frac{h-40}{h-40 \sqrt{3}}$
$\Rightarrow(2+\sqrt{3})(h-40 \sqrt{3})=h-40$
$\Rightarrow 2 h-80 \sqrt{3}+\sqrt{3} h-120=h-40$
$\Rightarrow h+\sqrt{3} h=80+80 \sqrt{3}$
$\Rightarrow(\sqrt{3}+1) h=80(\sqrt{3}+1)$
$\therefore h=80 \mathrm{~m}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.