The angle of elevation of the top of a tower 30 m

Let distance between the two towers = AB = x m

and height of the other tower = PA = h m

Given that, height of the tower = QB = 30 m and ∠QAB = 60°, ∠PBA = 30°

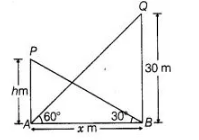
Now, in $\triangle Q A B, \quad \tan 60^{\circ}=\frac{Q B}{A B}=\frac{30}{x}$

$\Rightarrow \quad \sqrt{3}=\frac{30}{x}$

$\therefore$ $x=\frac{30}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}}=\frac{30 \sqrt{3}}{3}=10 \sqrt{3} \mathrm{~m}$

and in $\triangle P B A$, $\tan 30^{\circ}=\frac{P A}{A B}=\frac{h}{x}$

$\Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{h}{10 \sqrt{3}}$ $[\because x=10 \sqrt{3} \mathrm{~m}]$

$\Rightarrow \quad h=10 \mathrm{~m}$

Hence, the required distance and height are 10√3 m and 10 m, respectively.