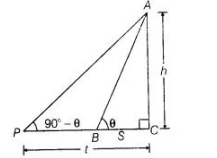
The angle of elevation of the top of a tower

Let the height of the tower is h.

and                                  ∠ABC = θ

Given that,                             BC = s, PC =t

and angle of elevation on both positions are complementary.

i.e ,                                 ∠APC = 90°- θ

[if two angles are complementary to each other, then the sum of both angles is equal to $\left.90^{\circ} .\right]$

Now in $\triangle A B C$. $\tan \theta=\frac{A C}{B C}=\frac{h}{s}$ .....(i)

 and in $\triangle A P C$

$\tan \left(90^{\circ}-\theta\right)=\frac{A C}{P C}$$\left[\because \tan \left(90^{\circ}-\theta\right)=\cot \theta\right]$

$\Rightarrow$ $\cot \theta=\frac{h}{t}$

$\Rightarrow$ $\frac{1}{\tan \theta}=\frac{h}{t}$ $\left[\because \cot \theta=\frac{1}{\tan \theta}\right]$ .......(ii)

On, multiplying Eqs. (i) and (ii), we get

$\tan \theta \cdot \frac{1}{\tan \theta}=\frac{h}{s} \cdot \frac{h}{t}$

$\Rightarrow$ $\frac{h^{2}}{s t}=1$

$\Rightarrow$ $h^{2}=s t$

$\Rightarrow$ $h=\sqrt{s t}$

So, the required height of the tower is √st.

Hence proved.