The angles of elevation of the top of a tower from two points at distances

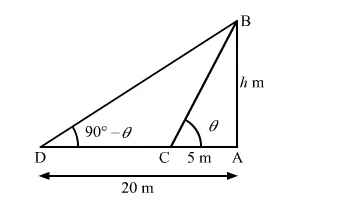
Let the height of the tower be AB.

We have,

$\mathrm{AC}=5 \mathrm{~m}, \mathrm{AD}=20 \mathrm{~m}$

Let the angle of elevation of the top of the tower (i.e. $\angle \mathrm{ACB}$ ) from point $\mathrm{C}$ be $\theta$. Then,

the angle of elevation of the top of the tower (i.e. $\angle \mathrm{ADB}$ ) from point $\mathrm{D}=\left(90^{\circ}-\theta\right)$

Now, in $\triangle \mathrm{ABC}$,

$\tan \theta=\frac{\mathrm{AB}}{\mathrm{AC}}$

$\Rightarrow \tan \theta=\frac{\mathrm{AB}}{5} \quad \ldots \ldots$ (i)

Also, in $\triangle \mathrm{ABD}$,

$\cot \left(90^{\circ}-\theta\right)=\frac{\mathrm{AD}}{\mathrm{AB}}$

$\Rightarrow \tan \theta=\frac{20}{\mathrm{AB}} \quad \ldots$. (ii)

From (i) and (ii), we get

$\frac{\mathrm{AB}}{5}=\frac{20}{\mathrm{AB}}$

$\Rightarrow \mathrm{AB}^{2}=100$

$\Rightarrow \mathrm{AB}=\sqrt{100}$

$\therefore \mathrm{AB}=10 \mathrm{~m}$

So, the height of the tower is 10 m.