The area of a trapezium is 475 cm2 and its height is 19 cm.

In the given figure, ABCD is a trapezium with parallel sides AB and CD.

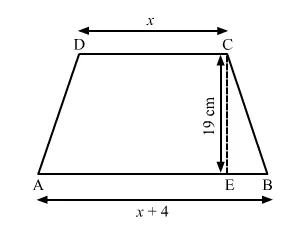
Let the length of CD be x.
Then, the length of AB be x + 4.

Area of trapezium $=\frac{1}{2} \times$ sum of parallel sides $\times$ height

$\Rightarrow 475=\frac{1}{2} \times(x+x+4) \times 19$

$\Rightarrow 475 \times 2=19(2 x+4)$

$\Rightarrow 950=38 x+76$

$\Rightarrow 38 x=950-76$

$\Rightarrow 38 x=874$

$\Rightarrow x=\frac{874}{38}$

$\Rightarrow x=23$

∴ The length of CD is 23 cm and the length of AB is 27 cm.

Hence, the lengths of two parallel sides is 23 cm and 27 cm.