The area of an equilateral triangle $\mathrm{ABC}$ is $17320.5 \mathrm{~cm}^{2}$. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle. Find the area of the shaded region.
(Use $\pi=3.14$ and $\sqrt{\mathbf{3}}=1.73205$ )
Area of the $\triangle \mathrm{ABC}$ (equilateral) $=17320.5 \mathrm{~cm}^{2}$
Let the side of the equilateral $\triangle \mathrm{ABC}$ be $\mathrm{x} \mathrm{cm}$.
Then, $\frac{\sqrt{3}}{4} \times x^{2}=17320.5$
$\Rightarrow \frac{1.73205}{4} \times x^{2}=17320.5(\because \sqrt{3}=1.73205)$
$\Rightarrow x^{2}=40000 \Rightarrow x=200 \mathrm{~cm}$
Then, radius of each circle = 100 cm.
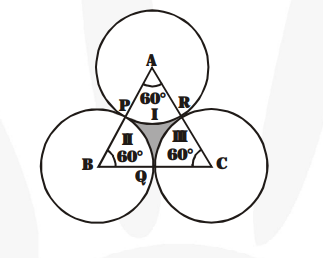
Area of the sector APR
$=\frac{\mathbf{C D}}{\mathbf{3 6 0}} \times \pi \times(100)^{2} \mathrm{~cm}^{2}=\frac{\pi}{\mathbf{6}} \times \mathbf{1 0 0 0 0} \mathbf{~ c m}^{2}$
Similarly, area of the sector BPQ = area of the sector CQR
$=\frac{\pi}{6} \times 10000 \mathrm{~cm}^{2}$
Total area of regions I, II and III (i.e., non-shaded region of $\triangle \mathrm{ABC}$ )
$=3 \times \frac{\pi}{\mathbf{6}} \times \mathbf{1 0 0 0 0} \mathrm{cm}^{2}=\frac{\mathbf{1}}{\mathbf{2}} \times 3.14 \times 10000 \mathrm{~cm}^{2}$
$=15700 \mathrm{~cm}^{2}$
Then, the required area of the shaded region of $\triangle \mathrm{ABC}$
$=17320.5 \mathrm{~cm}^{2}-15700 \mathrm{~cm}^{2}=1620.5 \mathrm{~cm}^{2}$