The area of the circle

The given equations are

$x^{2}+y^{2}=16$      ...(1)

$y^{2}=6 x$                ...(2)

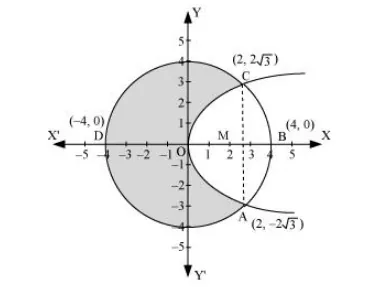
Area bounded by the circle and parabola

$=2[\operatorname{area}(\mathrm{OADO})+\operatorname{area}(\mathrm{ADBA})]$

$=2\left[\int_{0}^{2} \sqrt{6 x} d x+\int_{2}^{4} \sqrt{16-x^{2}} d x\right]$

$=2 \int_{0}^{2} \sqrt{6 x} d x+2 \int_{2}^{4} \sqrt{16-x^{2}} d x$

$=2 \sqrt{6} \int_{0}^{2} \sqrt{x} d x+2 \int_{2}^{4} \sqrt{16-x^{2}} d x$

$=2 \sqrt{6} \times \frac{2}{3}\left[x^{\frac{3}{2}}\right]_{0}^{2}+2\left[\frac{x}{2} \sqrt{16-x^{2}}+\frac{16}{2} \sin ^{-1}\left(\frac{x}{4}\right)\right]_{2}^{4}$

$=\frac{4 \sqrt{6}}{3}(2 \sqrt{2}-0)+2\left[\left\{0+8 \sin ^{-1}(1)\right\}-\left\{2 \sqrt{3}+8 \sin ^{-1}\left(\frac{1}{2}\right)\right\}\right]$

$=\frac{16 \sqrt{3}}{3}+2\left[8 \times \frac{\pi}{2}-2 \sqrt{3}-8 \times \frac{\pi}{6}\right]$

$=\frac{16 \sqrt{3}}{3}+2\left(4 \pi-2 \sqrt{3}-\frac{4 \pi}{3}\right)$

$=\frac{16 \sqrt{3}}{3}+8 \pi-4 \sqrt{3}-\frac{8 \pi}{3}$

$=\frac{16 \sqrt{3}+24 \pi-4 \sqrt{3}-8 \pi}{3}$

$=\frac{16 \pi+12 \sqrt{3}}{3}$

$=\frac{4}{3}[4 \pi+\sqrt{3}]$ square units

Area of circle $=\pi(r)^{2}$

$=\pi(4)^{2}$

$=16 \pi$ square units

$\therefore$ Required area $=16 \pi-\frac{4}{3}(4 \pi+\sqrt{3})$

$=16 \pi-\frac{16 \pi}{3}-\frac{4 \sqrt{3}}{3}$

$=\frac{32 \pi}{3}-\frac{4 \sqrt{3}}{3}$

$=\frac{4}{3}[8 \pi-\sqrt{3}]$ square units

Thus, the correct answer is C.