Question:
The area of the largest triangle that can be inscribed in a semi-circle of radius r is
(a) $2 r$
(b) $r^{2}$
(c) $r$
(d) $\sqrt{r}$
Solution:
The triangle with the largest area will be symmetrical as shown in the figure.
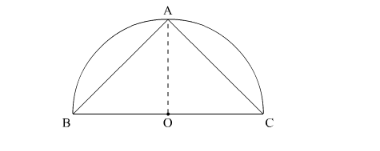
Let the radius of the circle be r.
Hence,
$\operatorname{ar}(\triangle \mathrm{ABC})=\frac{1}{2}(r)(2 r)$
$=r^{2}$ sq. unit
Therefore the answer is (b).
