The areas of two similar triangles are 81 cm2 and 49 cm2, respectively. If the altitude of one triangle is 6.3 cm,

It is given that the triangles are similar.
Therefore, the ratio of the areas of these triangles will be equal to the ratio of squares of their corresponding sides.
Also, the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
Let the two triangles be ABC and DEF with altitudes AP and DQ, respectively. 

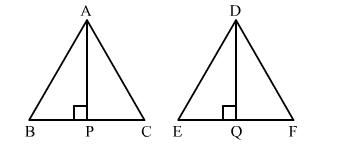
$\frac{\operatorname{ar}(\Delta A B C)}{\operatorname{ar}(\Delta P Q R)}=\frac{A P^{2}}{D Q^{2}}$

$\Rightarrow \frac{81}{49}=\frac{6.3^{2}}{D Q^{2}}$

$\Rightarrow D Q^{2}=\frac{49}{81} \times 6.3^{2}$

$\Rightarrow D Q^{2}=\sqrt{\frac{49}{81} \times 6.3 \times 6.3}$

$=4.9 \mathrm{~cm}$

Hence, the altitude of the other triangle is 4.9 cm.