The base of an equilateral triangle with side 2a lies along they y-axis such that the mid point of the base is at the origin.

Let ABC be the given equilateral triangle with side 2a.

Accordingly, AB = BC = CA = 2a

Assume that base BC lies along the y-axis such that the mid-point of BC is at the origin.

i.e., BO = OC = a, where O is the origin.

Now, it is clear that the coordinates of point C are (0, a), while the coordinates of point B are (0, –a).

It is known that the line joining a vertex of an equilateral triangle with the mid-point of its opposite side is perpendicular.

Hence, vertex A lies on the y-axis.

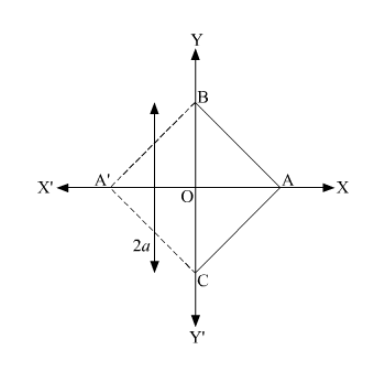
On applying Pythagoras theorem to $\triangle \mathrm{AOC}$, we obtain

$(\mathrm{AC})^{2}=(\mathrm{OA})^{2}+(\mathrm{OC})^{2}$

$\Rightarrow(2 a)^{2}=(\mathrm{OA})^{2}+a^{2}$

$\Rightarrow 4 a^{2}-a^{2}=(\mathrm{OA})^{2}$

$\Rightarrow(\mathrm{OA})^{2}=3 a^{2}$

$\Rightarrow \mathrm{OA}=\sqrt{3} a$

$\therefore$ Coordinates of point $\mathrm{A}=(\pm \sqrt{3} a, 0)$

Thus, the vertices of the given equilateral triangle are $(0, a),(0,-a)$, and $(\sqrt{3} a, 0)$ or $(0, a),(0,-a)$, and $(-\sqrt{3} a, 0)$.