The circumcentre of the ΔABC is 0.

Given A circle is circumscribed on a ΔABC having centre O.

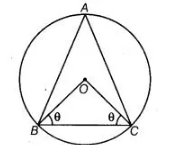
To prove $\quad \angle O B C+\angle B A C=90^{\circ}$

Construction Join $B O$ and $C O$.

Proof Let $\angle O B C=\angle O C B=\theta$  $\ldots(i)$

In $\triangle O B C, \quad \angle B O C+\angle O C B+\angle C B O=180^{\circ}$

[by angle sum property of a triangle is $180^{\circ}$ ]

$\Rightarrow \quad \angle B O C+\theta+\theta=180^{\circ}$

$\Rightarrow \quad \angle B O C=180^{\circ}-2 \theta$

We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.

$\therefore \quad \angle B O C=2 \angle B A C$

$\Rightarrow \quad \angle B A C=\frac{\angle B O C}{2}=\frac{180^{\circ}-2 \theta}{2}=90^{\circ}-\theta$

$\Rightarrow \quad \angle B A C+\theta=90^{\circ}$

$\therefore \quad \angle B A C+\angle O B C=90^{\circ} \quad$ [from Eq. (i)]

Hence proved.