Question:
The coefficient of $x^{-17}$ in the expansion of $\left(x^{4}-\frac{1}{x^{3}}\right)^{15}$ is
(a) 1365
(b) −1365
(c) 3003
(d) −3003
Solution:
(b) −1365
Suppose the $(r+1)$ th term in the given expansion contains the coefficient of $x^{-17}$.
Then, we have :
$T_{r+1}={ }^{15} C_{r}\left(x^{4}\right)^{15-r}\left(\frac{-1}{x^{3}}\right)^{r}$
$=(-1)^{r}{ }^{15} C_{r} x^{60-4 r-3 r}$
For this term to contain $x^{-17}$, we must have :
$60-7 r=-17$
$\Rightarrow 7 r=77$
$\Rightarrow r=11$
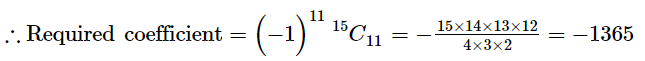
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
